Binary tree

Posted on Edited on In Disqus:
Introduction a data structure called binary tree, and how to traverse it.

定义

二叉树(Binary Tree)是一种数据结构，它的每个父节点(parent)至多有两个子节点(children)，分别被称为左孩子(the left child)和右孩子(the right child).

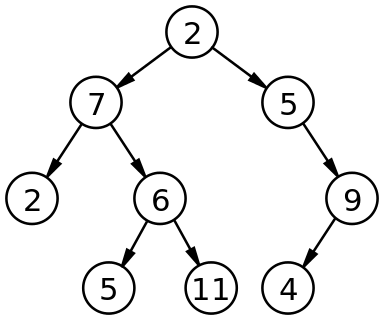
如上图所示, 该二叉树的大小(size)为9且高度(height)为3，根结点(root)的值为2. 另外，这是一棵不平衡(unbalanced)且未排序(unsorted)的二叉树。


特殊二叉树

  • 满二叉树(full binary tree)

    • 除叶子节点(leaf)外，所有分支节点都含有2个非空子节点的二叉树

    • 满二叉树上的节点要么有0个子节点，要么有2个子节点

    • 满二叉树的子树(subtree)是单个顶点(vertex)，或同样是满二叉树

  • 完全二叉树(complete binary tree)

    • 除了最后一层，其余层都是“满”的，且叶子节点尽可能向左靠齐

    • or 在最后一层中，移除最右边的叶子节点(rightmost leaves)

    • 完全二叉树节点总数在1 ～ $2^h$ 之间，其中h为树的高度

  • 完美二叉树(perfect binary tree)
    • 完全二叉树 + 满二叉树

二叉树属性

  • 在任意二叉树中，度数为2节点的个数等于叶子节点的个数减1

节点的度数等于其子节点的个数。因此，在二叉树中，节点的度数只可能为0，1和2。

当只有1个节点时，度为0。接着，每多出1个节点，同时会派生出1度。派生出的度和派生出的节点数一定相等。即：

节点总数 = 总度数 + 1

假设在一棵二叉树中，度数为2的节点数为X2，度数为1的节点数为X1，度数为0的节点数为X0。结合上式：

X2 + X1 + X0 = 2X2 + X1 + 1，推出 X2 = X0 - 1

因此，度数为2的节点个数等于叶节点数减1

  • 满二叉树定理：非空满二叉树的叶节点数等于其分支节点数加1

证明同上。在满二叉树中，度数为1的节点数为0。

  • 一颗非空二叉树中，空子树的数目等于其节点数目加1

当仅有根节点时：二叉树有2个空子树，1个节点，结论成立。

接着，空子树和节点等量增长，结论成立。

  • 满二叉树最少有2h+1个节点，最多有2^(h+1)-1个节点 (仅有根节点的二叉树的高度为0)
  • 在完美二叉树中，假设叶子结点的个数为l，高度为h，则l=2^h，总结点个数n=2^(h+1)-1

二叉树算法

二叉树的结点

1
2
3
4
5
6
7
template <class elemType>
struct binaryTreeNode
{
    elemType info;
    binaryTreeNode<elemType> *left;
    binaryTreeNode<elemType> *right;
};

二叉树的高度

1
2
3
4
5
6
7
8
template <class elemType>
int height(binaryTreeNode<elemType> *btn)
{
    if (btn == NULL)
        return 0;
    else
        return 1 + max(height(btn->left), height(btn->right));
}

二叉树的复制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
template <class elemType>
void copyTree(binaryTreeNode<elemType>* &copiedTreeRoot,
		binaryTreeNode<elemType>* otherTreeRoot)
{
    if (otherTreeRoot == NULL) {
        copiedTreeRoot = NULL;
    }
    else {
        copiedTreeRoot = new binaryTreeNode<elemType>;
        copiedTreeRoot->info = otherTreeRoot->info;
        copyTree(copiedTreeRoot->left, otherTreeRoot->left);
        copyTree(copiedTreeRoot->right, otherTreeRoot->right);
    }
}

二叉树的遍历 (traverse)

  • 前序遍历：根->左->右
  • 中序遍历：左->根->右
  • 后序遍历：左->右->根
递归遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//前序遍历
template <class elemType>
void preorder(binaryTreeNode<elemType> *btn)
{
    if (btn == NULL)  return;
    cout << btn->info << " ";
    preorder(btn->left);
    preorder(btn->right);
}

//中序遍历
template <class elemType>
void inorder(binaryTreeNode<elemType> *btn)
{
    if (btn == NULL)  return;
    inorder(btn->left);
    cout << btn->info << " ";
    inorder(btn->right);
}

//后序遍历
template <class elemType>
void postorder(binaryTreeNode<elemType> *btn)
{
    if (btn == NULL)  return;
    postorder(btn->left);
    postorder(btn->right);
    cout << btn->info << " ";
}
迭代遍历

需要额外的一个栈stack结构来辅助实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
//前序遍历
template <class elemType>
void preorderIteration(binaryTreeNode<elemType> *root)
{
    stack<binaryTreeNode<elemType>*> st;
    if(root)
        st.push(root);

    while(!st.empty()){
        binaryTreeNode<elemType> *cur = st.top();
        st.pop();

        cout << cur->info << " ";//操作当前节点

        if(cur->right)
            st.push(cur->right);
        if(cur->left)
            st.push(cur->left);
    }
}

//中序遍历
template <class elemType>
void inorderIteration(binaryTreeNode<elemType> *root)
{
    stack<binaryTreeNode<elemType>*> st;

    binaryTreeNode<elemType> *cur = root;

    while(cur || !st.empty()){
        if(cur){
            st.push(cur);
            cur = cur->left;
        }
        else{
            cur = st.top();
            st.pop();

            cout << cur->info << " ";//操作当前节点

            cur = cur->right;
        }
    }
}

//后序遍历
template <class elemType>
void postorderIteration(binaryTreeNode<elemType> *root)
{
    stack<binaryTreeNode<elemType>*> st;
    binaryTreeNode<elemType> *pre;

    if(root)
        st.push(root);

    while(!st.empty()){
        binaryTreeNode<elemType> *cur = st.top();
        /*
         * 出栈条件：
         * 对于叶子节点：直接弹出
         * 对于非叶子节点：如果已经遍历过其左子节点或右子节点，则弹出
         */
        if((!cur->left && !cur->right) || (pre && (cur->left == pre || cur->right == pre))){
            st.pop();
            cout << cur->info << " ";//操作当前节点
            pre = cur;
        }
        else{//说明是一个非叶子节点，并且还未访问其左右孩子
            if(cur->right)
                st.push(cur->right);
            if(cur->left)
                st.push(cur->left);
        }
    }
}

需要额外的一个队列queue结构来辅助实现。

大致思想为：队列初始化时只有根节点，每个节点出队列时，将它子节点加入队列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
template <class elemType>
void BFS(binaryTreeNode<elemType>* btn) {
    if(btn == nullptr)
        return;
	
    queue<binaryTreeNode<elemType> *> que; //构造一个树结点指针的队列
    que.push(btn);
 
    while(!que.empty()){
        binaryTreeNode<elemType> *q = que.front();
        cout << q->info << " ";
        que.pop();
		
        if(q->left != nullptr)  //左子节点入队列
            que.push(q->left);
        if(q->right != nullptr)  //右子节点入队列
            que.push(q->right);
    }
}

二叉树的算法思路：仅考虑当前结点的任务，将其余部分交给递归或迭代框架。其算法框架大致为：

1
2
3
4
5
6
7
8
9
template <class elemType>
void BTFramework(binaryTreeNode<elemType>* btn, int target) {
    if (btn->val == target)
        DoSometing;
    if (btn->left != nullptr)
        BTFramework(btn->left, target);
    if (btn->right != nullptr)
        BTFramework(btn->right, target);
}

这个以后再细说。。。

代码下载地址：https://xiaoli777.github.io/codes/BinaryTree.cpp